
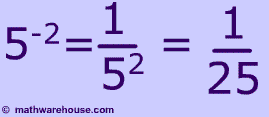
Springer-Handbuch der Mathematik I (in German).

Department of Commerce, Cambridge University Press. National Institute of Standards and Technology (NIST), U.S. Note this is not the same as 2 √3 3, which equals 3. When raising a number to a negative exponent, use the reciprocal of the base and make the exponent sign positive:Īnother way of writing a base raised to a fraction is to take the denominator root of the base and raise it to the numerator power:Ĭheck your math, since you know 3 3/2 = 3 1.5. (2 3) 2 = 2 3×2 = 2 6 Negative Exponent Rule When raising a power by another power, keep the base and multiply the exponents together: Distribute the exponent to all values within the brackets: X -3/x 2 = x (-3-2) = x -5 Power of a ProductĪnother way of expressing a base multiplied by an exponent is distributing the exponent to each base:ĭistribution works when dividing numbers, too. Similarly, divide exponents with the same base by keeping the base and subtracting the exponents: When you multiply exponents with the same base, keep the base add the exponents: However, if the base is 0, matters become complicated. Knowing this rule can save you a lot of pointless calculation! So, no matter how complicated the base is, if you raise it to the zero power, it equals 1. One helpful exponent rule is that any non-zero number raised to the zero power equals 1: For example:Ģx 3y 2 + 4x 3y 2 = 6x 3y 2 Zero Exponent Rule You can add and subtract numbers with exponents, but only when the base and exponent of the terms are the same. Understanding the rules for exponents makes working with them much easier. This is why they find use in scientific notation. (x)(x)(x)(y)(y) = x 3y 2 Exponent Rules and ExamplesĮxponents simplify writing extremely large or very small numbers.

For instance, here is an expanded form and exponential form of an equation using x and y: Many time, exponents combine with algebra. So, 5 3 is “five cubed.” A number raised to the power of 2 is “squared.” You can read the expression 5 3 as “five raised to the third power” or “five raised to the power of three.” However, a number raised to the power of 3 is generally read as “cubed”. In order to respect the 'exponents add' rule, it must be the case that +. Consider the question of what should mean. Here, the number 5 is the base and the number 3 is the exponent or power. The rule that multiplying makes exponents add can also be used to derive the properties of negative integer exponents. Reading and Writing Exponentsįor example, 5 3 = (5)(5)(5) = 125. It is a shorthand for repeated multiplication that makes writing equations simpler. An exponent means repeated multiplication.Īn exponent or power is a superscript over a number (the base) that tells how many times you multiple that number by itself.


 0 kommentar(er)
0 kommentar(er)
